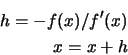


Next: Cenni sulle classi ed
Up: Un po' di esercizi
Previous: Esercizio 5
Indice
Esiste il metodo di Newton per calcolare uno zero di una funzione
in un intervallo dato. Per esempio se abbiamo 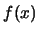 in [a,b] e
sappiamo che sia
in [a,b] e
sappiamo che sia 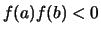 implica che esiste almeno un punto
implica che esiste almeno un punto 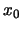 in cui la nostra funzione è uguale a zero. Il procedimento
di Newton si basa sul fatto che se ci spostiamo da un punto iniziale
in cui la nostra funzione è uguale a zero. Il procedimento
di Newton si basa sul fatto che se ci spostiamo da un punto iniziale
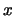 in un punto
in un punto 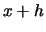 prossimo al nostro zero della funzione
prossimo al nostro zero della funzione 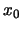 (
(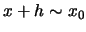 ) si ha
) si ha
ossia da 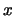 posso scegliere
posso scegliere 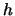 e aggiornare il mio nuovo
e aggiornare il mio nuovo 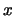 come
come
in questo modo iterativamante ci muoviamo verso il valore 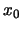 .
L'algoritmo di Newton è molto efficiente per calcolare la
radice di un numero. Se infatti vogliamo calcolare la
radice di un numero
.
L'algoritmo di Newton è molto efficiente per calcolare la
radice di un numero. Se infatti vogliamo calcolare la
radice di un numero 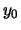 possiamo considerare la funzione
possiamo considerare la funzione
che si annulla esattamente quando il valore di 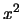 eguaglia
eguaglia 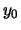 ,
ossia quando
,
ossia quando 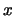 diviena la radice di
diviena la radice di 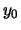 .
.
Esercizio: scrivere una funzione che implementi il metodo
di Newton e calcolare la radice di un numero positivo.
Un esempio di soluzione può essere
def newton(f,df,a,b,y,tol):
''' newton(f,df,a,b,y,tol)
find the square root of y in the interval a,b starting from (a+b)/2
'''
maxcount=100000 # maximun number of step
count=0
x=(a+b)/2.0 # starting point
while (f(x,y)>tol) and (count<maxcount):
h=-f(x,y)/df(x)
x = x + h
count = count + 1
return x
def f(x,y0):
''' f(x) = x*x '''
return x*x - y0
def df(x):
''' df(x) = 2*x '''
return 2.0*x
if __name__ == '__main__':
import math
tolerance = 0.0001
y0=input('sqrt of = ')
print "math ",y0,math.sqrt(y0),"computed",newton(f,df,0,y0,y0,tolerance)



Next: Cenni sulle classi ed
Up: Un po' di esercizi
Previous: Esercizio 5
Indice
2004-11-02