Algoritmo di Needlman-Wunsh

Anche se l'algoritmo presentato in questo paragrafo non è, l'algoritmo che presentarono per la prima volta Needlman-Wunsh nel 1970 sulla rivista J. Mol. Biol., è entrato nell'uso comune riferirsi ad esso come il metodo per calcolare il costo di un allineamento globale a coppie.

Dal capitolo precedente noi abbiamo appreso che esiste una tecnica (programmazione dinamica), che per mezzo della risoluzione dei sotto-problemi, di cui viene mantenuta traccia, permette di risolvere il problema globale. In particolare, si può notare che il problema dell'allineamento di due sequenze è analogo al problema della massima sottosequenza comune, che è stato trattato nel Capitolo . Dal che si deduce che per risolvere il problema del calcolo di un $BA$, non dobbiamo esplorare tutte le numerosissime soluzioni, ma ci si può affidare alla programmazione dinamica.

Prima di passare alla risoluzione del nostro problema, introduciamo la seguente notazione. Indichiamo con $s_{i,j}$ la sottosequenza di $s$ che parte dalla posizione $i$ inclusa e termina alla posizione $j$ inclusa. L'analogo in Python è $s_{i,j}$ = s[i:j+1].

Definita una misura di distanza ($M(i,j)$, $D(i,-)$ e $I(-,j)$), la soluzione del problema, si ottiene facendo le seguenti considerazioni. Date due sequenze $s$ e $t$, di cui vogliamo calcolare il costo di un allineamento ottimo, di può notare che: se abbiamo risolto il problema di trovare gli allineamenti ottimi tra le sotto-sequenze

1. $s_{0,i-1}$ e $t_{0,j-1}$ (costo = $C(s_{0,i-1},t_{0,j-1})$)
2. $s_{0,i-1}$ e $t_{0,j}$ (costo = $C(s_{0,i-1},t_{0,j})$)
3. $s_{0,i}$ e $t_{0,j-1}$ (costo = $C(s_{0,i},t_{0,j-1})$)

allora un allineamento ottimo tra le due sequenze $s_{0,i}$ e $t_{0,j}$ può essere ottenuto soltanto in uno dei tre possibili modi

1. $C(s_{0,i-1},t_{0,j-1}) + M(i,j)$
2. $C(s_{0,i-1},t_{0,j}) + D(i,-)$
3. $C(s_{0,i},t_{0,j-1}) + I(-,j)$

e noi sceglieremo il minimo tra i tre.

Per esempio se vogliamo ottenere il costo di un allineamento ottimo tra le sequenze $s$="FKLA" e $t$="FKSTLA", il costo dell'allineamento fino alla posizione $C(s_{0,2},t_{0,2})$=$C$(FKL,FKS), sarà

$$\begin{eqnarray*} C(FKL,FKS) = min \{ C(FK,FK) + M(L,S), \\ C(FK,FKS) + D(L,-), \\ C(FKS,FK) +I(-,S) \} \end{eqnarray*}$$

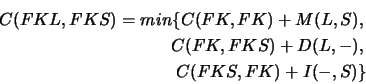
che rappresenta la scelta di minimo costo tra

        Caso 1:              Caso 2:             Caso 3:
    pos_s.....i          pos_s.....i         pos_s....i.
        s: ...L              s: ...L             s: ...- 
        t: ...S              t: ...-             t: ...S
    pos_t.....j          pos_t....j.         pos_t.....j

Siccome si vuole mantenere la simmetria tra la sequenza $s$ e quella $t$, si pone $D(i,-)=I(-,j)=f(gap)$. Una semplice scelta è quella di porre il costo del gap costante a crescita lineare, ossia si fissa $D(i,-)=I(-,j)= g$. In questo caso avremmo che il calcolo del costo di un allineamento diviene

$$\begin{eqnarray*} C(i,j) = min\{ C(i-1,j-1) + M(i,j), \\ C(i-1,j)+g, \\ C(i,j-1)+g \} \end{eqnarray*}$$

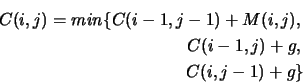
dal punto di vista grafico, significa, che dobbiamo avere una matrice con $C$ di dimensione $(len(s)+1) \times (len(t)+1)$, che dobbiamo riempire seguendo la regola

$$\begin{eqnarray*} C(i-1,j-1) &\quad &C(i-1,j) \\ \quad &_{(match)}\searrow & \downarrow^{(gap)} \\ C(i,j-1) &_{ (gap)}\rightarrow & [C(i,j)] \end{eqnarray*}$$

Per poter procedere al computo completo abbiamo bisogno anche di quelle che vengono chiamate condizioni al contorno. Esse rappresentano il peso che diamo all'allineamento della sequenza $s$ contro tutti gaps $-$, e alla sequenza $t$ contro tutti i gaps $-$. In pratica per l'algoritmo che stiamo considerando, vogliamo che il costo dei singoli gaps, cresca linearmente con l'aumentare del numero. Da cui si ha

• $C(0,0) = 0$ (valore iniziale)
• $C(i,0) = C(i-1,0) + g$, con $i=1$ to $len(s)+1$ (prima sequenza contro soli gaps)
• $C(0,j) = C(0,j-1) + g$, con $j=1$ to $len(t)+1$ (seconda sequenza contro soli gaps)

A questo punto siamo in grado di calcolare il costo minimo del nostro allineamento globale, basandoci sul calcolo della distanza minima. In Figura , viene riportato tale algoritmo. Come si può notare dalla Figura , il costo di un allineamento ottimo è contenuto nell'ultima casella della matrice C. Osservando Figura e in particolare i punti #(1) e #(2), si può verificare che la complessità computazionale dell'algoritmo è, nello spazio occupato

$$Comp_{spazio}=O(m\cdot n)$$

nel tempo

$$T=O(m\cdot n) = (con \quad m \sim n) = O(n^2)$$

dove con $m=len(s)$ e $n=len(t)$. Abbiamo perciò ottenuto che a dispetto del fatto che esistano un numero di allineamenti superiore a $e^n$, utilizzando la programmazione dinamica otteniamo la soluzione in un tempo $O(n^2)$.

Figura: Calcolo del costo di un allineamento globlale basado sulla distanza

Se oltre al costo, si vuole anche ottenere un allineamento, allora abbiamo bisogno di mantenere traccia, del valore ottenuto. Questo significa che oltre la matrice dei costi $C$, dobbiamo utilizzare una matrice $B$ che tiene traccia del percorso fatto. Ossia, se la casella $C[i][j]$ è stata aggiornata utilizzando il match (diagonale $\searrow$), allora dobbiamo memorizzare il percorso nella matrice di backtrace, ponendo per esempio $B[i][j]='D'$. Analogamente per gli altri 2 casi, che sono: colonna ($\downarrow$) $B[i][j]='C'$ e riga ($\rightarrow$) $B[i][j]='R'$. L'algoritmo global_dist_al deve quindi essere modificato come riportato in Figura .

La procedura per poter ottenere un allineamento data la matrice di backtrace $B$, la si può meglio comprendere utilizzando l'esempio riportato in Figura , dove si suppone di partire da una determinata cella i,j della matrice di backtrace e di trovare nella matrice le solite 3 possibilità.

Figura: Esempio di ricostruzione di un allineamento

Un possibile algoritmo per la ricostruzione di un allineamento data la matrice di backtrace $B$, è descritto in Figura . Esso richiede in input la matrice di backtrace B, le due sequenze seq1, seq2 e restituisce due sequenze lunghe uguali e pari alla lunghezza dell'allineamneto specificato dalla matrice B. Ovviamente in questo caso le due sequnze possono includere il simbolo di gap (gap_symbol='-').

Come si nota facilmente dal codice (Figura ), get_global_alignment implementa ciò che avevamo descritto in Figura . Ossia quando ci si muove lungo la diagonale, si ha un 'match', ed usiamo sia un simbolo della sequenza $s$, che uno della sequenza $t$. Al contrario, quando ci si muove lungo la colonna, consumiamo solo un simbolo della sequenza $s$, che appaiamo con un gap. Analogamente e in modo opposto nel caso in cui ci si muove lungo la riga (si consumano simboli in $t$ soltanto).

Si può notare che in realtà l'algoritmo di Figura è più generale, e permette qualsiasi funzione di score $M(a,b)$, nonché, il fatto di poter calcolare sia la minima distanza (minimo tra 3 valori), sia la massima similarità (massimo tra 3 valori). Per poter eseguire tale algorimo abbiamo bisogno di definire queste funzioni, ed un esempio semplice è dato in Figura . Se li utilizziamo per calcolare la minima distanza tra le sequenze "FKLA" e "FKSTLA", possiamo vedere il risultato in Tabella , in cui sono riportati i valori delle matrici e l'allineamento corrispondente ottenuto.

Fino ad ora ci siamo sempre espressi dicendo che dato il minimo costo (o massima similarità) tra due sequenze, volevamo ricostruire un allienamento con tale punteggio e non l'allienamento con punteggio massimo. Ciò è dovuto al fatto che, esistono casi ambigui, in cui vi possono essere più allineamenti con lo stesso valore di distanza (similarità). In questi casi di solito si seglie una strategia, che può essere di scegliere colonna, poi riga, ed infine diagonale (oppure variazioni a questo ordinamento). Come esempio di ambiguità, si può vedere il caso di della ricerca di minima distanza tra le due sequenze ACCA, e ACA. In Tabella , sono riportate le matrici del punteggio e quella di backtrace. Come si può notare entrambi gli allineamenti

s: AC-A
t: ACCA
oppure
s: A-CA
t: ACCA

sono corretti e corrispondono ad un costo minimo di 1.0.

Figura: Algoritmo per il computo di un allineamento globlale

Figura: Algoritmo per estrarre un allineamento ottimo

Figura: Esempio di funzione per il calcolo di $M(a,b)$ (id_score), e per il calcolo del massimo tra 3 valori (max3)

    
Score Matrix
    

Tabella: Le matrici di Score e backtrace per le sequenze "FKLA" e "FKSTLA"

	0	F	K	S	T	L	A
0	0.0	1.0	2.0	3.0	4.0	5.0	6.0
F	1.0	0.0	1.0	2.0	3.0	4.0	5.0
K	2.0	1.0	0.0	1.0	2.0	3.0	4.0
L	3.0	2.0	1.0	1.0	2.0	2.0	3.0
A	4.0	3.0	2.0	2.0	2.0	3.0	2.0

    
    
    
Backtrace Matrix
    

	0	F	K	S	T	L	A
0	0	R	R	R	R	R	R
F	C	D	R	R	R	R	R
K	C	C	D	R	R	R	R
L	C	C	C	D	D	D	R
A	C	C	C	D	D	D	D

    
    
    
Obtained Alignment
    

s: FK-LA

t: FKSTLA

    
Score Matrix
    

Tabella: Le matrici di score e backtrace per le sequenze "ACA" e "ACCA"

	0	A	C	C	A
0	0.0	1.0	2.0	3.0	4.0
A	1.0	0.0	1.0	2.0	3.0
C	2.0	1.0	0.0	$^{\searrow} _{\rightarrow}$1.0	2.0
A	3.0	2.0	1.0	1.0	1.0

    
    
    
Backtrace Matrix
    

	0	A	C	C	A
0	0	R	R	R	R
A	C	D	R	R	D
C	C	C	D	R/D	R
A	C	D	C	D	D

    
    
    
Obtained Alignments
    

Caso Riga $\rightarrow$

s: AC-A

t: ACCA

Caso Diagonale $\searrow$

s: A-CA

t: ACCA