


Next: Massimizzazione di funzioni
Up: Modelli di Markov
Previous: Modelli di Markov
Indice
Esercizio 1.
Derivare le equazioni ![[*]](crossref.png) . Per derivare le equazioni vediamo prima che
il risultato è il medesimo utilizzando invecie della funzione
. Per derivare le equazioni vediamo prima che
il risultato è il medesimo utilizzando invecie della funzione 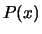 la funzione
la funzione
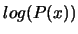 . Infatti se abbiamo una funzione
. Infatti se abbiamo una funzione 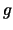 monotona crescente in un intervallo
monotona crescente in un intervallo
![$I = ] a,b [$](img372.png) , ossia
, ossia
allora si ha che i valori che annullano la derivata prima di una funzione 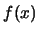 con
con 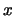 in
in 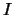 sono i medesimi che annullano la derivata prima di
sono i medesimi che annullano la derivata prima di 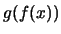 in
in 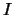 . Infatti
. Infatti
in quanto la definizione di 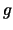 implica che
implica che
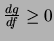 per
per 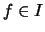 . Nel nostro
caso assumendo
. Nel nostro
caso assumendo
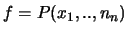 e cercando un massimo della probabilità
e cercando un massimo della probabilità 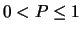 possiamo
prendere come
possiamo
prendere come 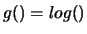 . e le equazioni si semplificano ottenendo
. e le equazioni si semplificano ottenendo
Nel caso della derivata rispetto a 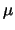 abbiamo
abbiamo
In modo analogo derivando cioè rispetto a 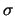 ricaviamo la
seconda delle equazioni
ricaviamo la
seconda delle equazioni ![[*]](crossref.png) .
.
2004-11-02
![[*]](crossref.png) . Per derivare le equazioni vediamo prima che
il risultato è il medesimo utilizzando invecie della funzione
. Per derivare le equazioni vediamo prima che
il risultato è il medesimo utilizzando invecie della funzione 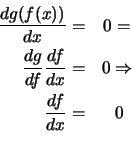
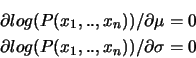
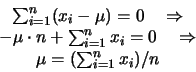
![[*]](crossref.png) .
.